I dusted off some old work and notes of mine on language models, and it inspired me to write up a brief overview that’s hopefully fit for public consumption.
A model, by definition, abstracts away unimportant aspects of the system that it simulates. When building and training a language model, we must consider how to map real- world factors to something quantifiable. In other words, we would reduce all the context inherent in a productive language system — its morphology, syntax, orthography, semantics and other linguistic factors — to a frequency distribution or some other metric.
Suppose that Alice looks at the domain name thenullstring.com and attempts to parse it. It’s possible that, reading from left to right, she might begin by mentally segmenting the first word as then and, examining her English lexicon, realize that the remaining ullstring has no reasonable segmentation. She might then backtrack and successfully segment the, null, and string in short order. Suppose, though, that she looks at (to give a somewhat famous albeit outdated¹ example) expertsexchange.com. One possible left-to-right segmentation is expert sex change; another is experts exchange. Which one is correct?
We as humans apply our world knowledge to hopefully parse this domain name as the latter segmentation rather than the former. This knowledge is deep, broad, and often unspoken, but we rely on it to choose experts exchange as being a more probable interpretation. A language model based on some corpus has no proximate access to that knowledge, but it may ultimately have access to the quantifiable consequences of that knowledge, namely that the term experts exchange is somewhat more probable than expert sex change, and that the null string is much more probable than then ullstring.
So what we’re after, then, is a means of assessing the probability of a sequence of words ![]() , or any word
, or any word ![]() within it based on known probabilities of those words either alone or in tandem with each other; in other words, we want a statistical language model. Generically, assuming a sequence of random variables
within it based on known probabilities of those words either alone or in tandem with each other; in other words, we want a statistical language model. Generically, assuming a sequence of random variables ![]() , the probability of such a sequence can be determined by the chain rule:
, the probability of such a sequence can be determined by the chain rule:
![]()
(1) 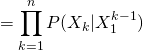
Given this, for the word sequence ![]() of length
of length ![]() being represented as
being represented as ![]() , we see:
, we see:
![]()
(2) 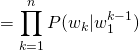
However, if ![]() is sufficiently large, the productivity of language dictates that for some
is sufficiently large, the productivity of language dictates that for some ![]() ,
, ![]() , which in turn causes our joint probability estimate to zero out as well. One way we can deal with this by assuming that our model is a Markov model, which is to say that we approximate the probability of a word
, which in turn causes our joint probability estimate to zero out as well. One way we can deal with this by assuming that our model is a Markov model, which is to say that we approximate the probability of a word ![]() by setting
by setting ![]() to be relatively small. For example, if a bigram model is given the test sequence Top Congressional leaders met with President, we calculate the probability of the next word being Obama as
to be relatively small. For example, if a bigram model is given the test sequence Top Congressional leaders met with President, we calculate the probability of the next word being Obama as ![]() , rather than
, rather than ![]() . This bigram model derives the probability of a given word by using the conditional probability of just the preceding word
. This bigram model derives the probability of a given word by using the conditional probability of just the preceding word ![]() rather than the conditional probability of all the preceding words in a sequence
rather than the conditional probability of all the preceding words in a sequence ![]() . In point of fact, by asserting that the probability of a word can be found by using either conditional probability, the bigram model states that the two conditional probabilities are approximately equivalent:
. In point of fact, by asserting that the probability of a word can be found by using either conditional probability, the bigram model states that the two conditional probabilities are approximately equivalent:
(3) ![]()
We’re making this bigram assumption for a single word, but we can go ahead and substitute Eq. (3) into Eq. (2) to get the probability of a sequence:
(4) 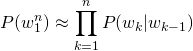
or, given some special sentence-delineating characters to ensure that bigram contexts are possible for all words:
![]()
![]()
![]()
“Okay,” you may be saying, “but how do you actually get the probability of any words to begin with?” This is where the corpus comes in. Suppose that we wanted to find ![]() : it would be a simple matter to count the number of occurrences of leaders to find its absolute frequency and to divide that number by the total number of tokens in the corpus to find its probability. But now suppose that we wanted to find
: it would be a simple matter to count the number of occurrences of leaders to find its absolute frequency and to divide that number by the total number of tokens in the corpus to find its probability. But now suppose that we wanted to find ![]() . We need to take into account the fact that Congressional might occur in many other contexts, such as Congressional aides, and we expressly don’t want to find anything but
. We need to take into account the fact that Congressional might occur in many other contexts, such as Congressional aides, and we expressly don’t want to find anything but ![]() . The thing to do here then is to count the occurrences of all bigrams beginning with Congressional in order to normalize to a relative frequency. We can see as a shortcut that the count of all such bigrams is the same as the count of the unigram Congressional. Thus, to find
. The thing to do here then is to count the occurrences of all bigrams beginning with Congressional in order to normalize to a relative frequency. We can see as a shortcut that the count of all such bigrams is the same as the count of the unigram Congressional. Thus, to find ![]() we simply divide the count of Congressional leaders by the count of Congressional. So for bigrams we see:
we simply divide the count of Congressional leaders by the count of Congressional. So for bigrams we see:
(5) ![]()
and more generally:
(6) 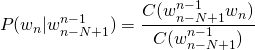
So far we’ve seen that with a source corpus yielding a frequency distribution on which to train, we can construct a simple language model that predicts the probability of a sequence of words based on its terms. I did engage in some hand-waving, though: I didn’t specify exactly how probabilities for words at the beginning and end of sentences can be computed, and generally I neglected the issue of what happens when a word in a test sequence doesn’t occur in the training data. A future post will look at these issues and examine how useful this modeling technique can be when attempting to automatically segment concatenated strings such as domain names.
¹ The domain has been renamed experts-exchange.com.

